Fully Homomorphic Encryption (FHE) in a Banking Quantum Era

Explore how Fully Homomorphic Encryption revolutionises data security in Banking and the Financial Industry, ensuring privacy against quantum computing threats.

Fully Homomorphic Encryption (FHE) promises to redefine data security in Banking and the Financial Industry. By enabling computations on encrypted data, FHE safeguards privacy against both conventional and quantum computing threats.

Introduction

The implementation of FHE in the financial sector is not just theoretical; it's becoming a practical reality, transforming data security and privacy standards. This article explores the practical uses, regulatory concerns, possible downsides, and research advancements of fully homomorphic encryption (FHE) in Finance and also Artificial Intelligence (AI) applications.

Understanding Fully Homomorphic Encryption

The Basics of Encryption

Encryption is a method of transforming readable data (plaintext) into an unreadable format (ciphertext) using an algorithm and an encryption key. The primary goal is to ensure that only authorised parties can access the original data by decrypting the ciphertext using a decryption key.

Traditional Encryption Methods

Traditional encryption methods can be broadly categorised into two types: symmetric and asymmetric encryption. Symmetric encryption employs a single key for both encryption and decryption. This efficiency comes at the cost of security, especially when key distribution poses challenges. Asymmetric encryption, also called public-key cryptography, uses two keys, one for encryption and another for decryption. This method is more secure but slower than symmetric encryption.

The Limitations of Conventional Encryption for Computation

While traditional encryption methods effectively secure data at rest or in transit, they fall short when it comes to performing computations on encrypted data. Typically, to process or analyse encrypted data, one must first decrypt it, perform the necessary operations, and then re-encrypt it. This decryption step poses a significant risk to data privacy, especially in untrusted or cloud computing environments.

The Breakthrough of Homomorphic Encryption

Homomorphic encryption (HE) solves the limitations of conventional encryption. It allows certain computations to be done directly on encrypted data (ciphertexts). The decrypted result is the same as the original data (plaintext) after the same operations are performed. HE comes in three main flavours: Partially Homomorphic Encryption (PHE), Somewhat Homomorphic Encryption (SHE), and Fully Homomorphic Encryption (FHE).

• Partially Homomorphic Encryption (PHE): Supports unlimited operations of a single type (e.g., either addition or multiplication) on ciphertexts.
• Somewhat Homomorphic Encryption (SHE): Supports a limited number of operations, combining both addition and multiplication, but only to a certain depth.
• Fully Homomorphic Encryption (FHE): The most advanced form, allowing for unlimited operations of both addition and multiplication on ciphertexts.

The Technical Ingenuity of FHE

FHE is based on complex mathematical structures, such as lattice-based cryptography. Lattice-based cryptography is a type of encryption that uses mathematical structures called lattices.

A lattice is a regular arrangement of points in space, and lattice-based cryptography relies on the difficulty of solving certain mathematical problems related to these structures. This makes lattice-based cryptography secure and resistant to attacks, including those from quantum computers.

In 2009, Craig Gentry developed a method, described in his paper A Fully Homomorphic Encryption Scheme ⧉, for creating a system that could perform homomorphic evaluation of its own decryption circuit. This self-referential design allows FHE schemes to perform arbitrary computations on encrypted data.

The FHE Algorithm Process

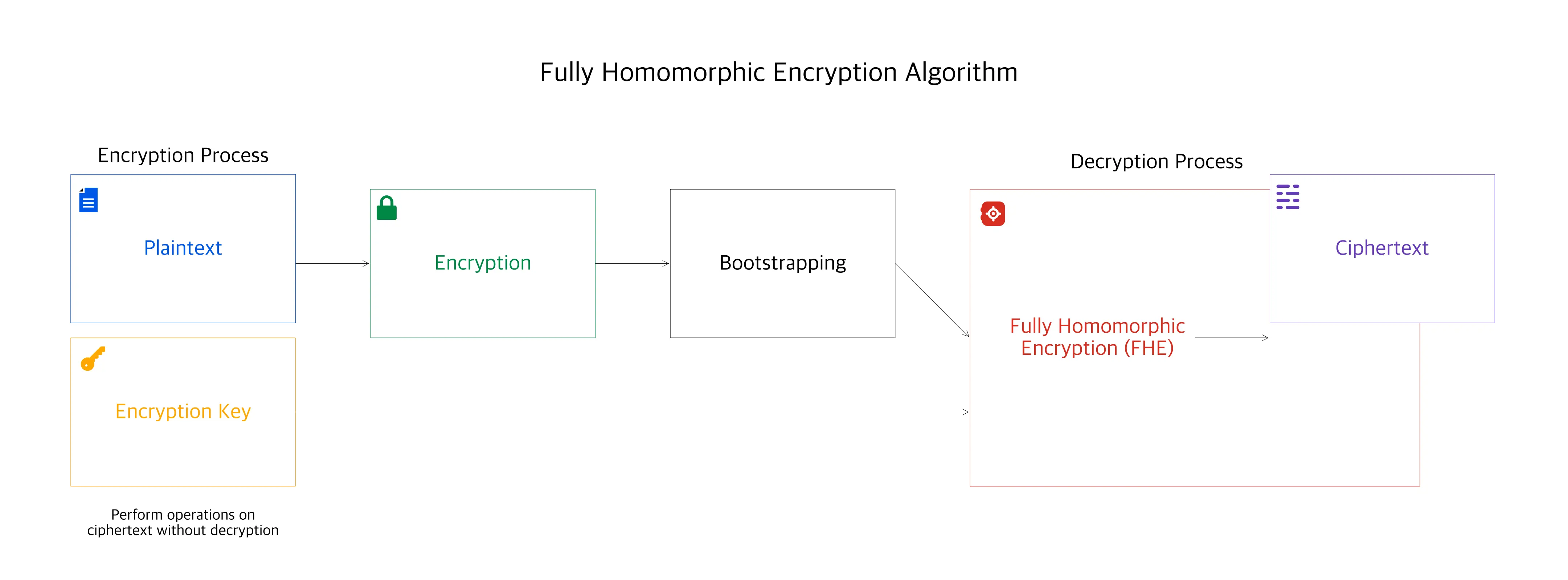
The diagram above illustrates the operational flow of a Fully Homomorphic Encryption (FHE) algorithm.

• The encryption process commences with the plaintext data, which is encrypted using an encryption key to generate ciphertext.

• This encrypted data can then undergo various computations directly on the ciphertext through a process known as bootstrapping.

• This unique capability of FHE allows data to remain encrypted throughout the entire process. Once the necessary operations have been performed, the decryption process can convert the modified ciphertext back into plaintext using the FHE scheme.

The primary advantage of FHE lies in its ability to perform computations on ciphertext without the need for decryption, thereby ensuring data privacy and security are maintained throughout the computation process.

The Quantum Resistance of FHE

Traditional encryption methods are often vulnerable to quantum algorithms. These algorithms can rapidly solve problems such as integer factorisation and discrete logarithms, which form the foundation of these encryption methods. In contrast, Fully Homomorphic Encryption (FHE) employs lattice-based problems that are believed to be challenging for quantum computers to solve. This quantum resistance makes FHE a promising encryption method for the post-quantum era.

Lattice-based FHE is resistant to quantum attacks because the underlying mathematical problems, such as the Shortest Vector Problem (SVP) and the Closest Vector Problem (CVP), are considered to be difficult to solve even for quantum computers. While quantum algorithms like Shor's algorithm can break traditional encryption methods that rely on factoring large numbers or computing discrete logarithms, they are not known to provide significant advantages in solving lattice-based problems. This characteristic makes lattice-based FHE a promising candidate for post-quantum cryptography.

The Impact of FHE on Banking and Finance

Enhanced Data Privacy and Security

The application of FHE in the financial sector promises a significant enhancement in data privacy. Banks can now undertake risk assessments, fraud detection, and comprehensive data analytics while ensuring the absolute confidentiality of customer information. This technological advancement mitigates the risk of data breaches, reinforcing the integrity of digital banking platforms and financial transactions.

Cloud Computing and Outsourcing

One major application area for homomorphic encryption is secure data processing in the cloud. Banks can leverage cloud computing services to process encrypted data without compromising data privacy. This enables financial institutions to harness the scalability and cost-efficiency of cloud computing while maintaining the confidentiality of sensitive financial information.

The shift towards cloud computing and outsourcing of computational tasks by banks underscores the relevance of FHE. With secure cloud computing, financial institutions can tap into external resources while protecting sensitive encrypted data through Fully Homomorphic Encryption (FHE). FHE enables banks to securely leverage cloud computing services while ensuring that sensitive encrypted data remains protected at all times.

Preparing for the Quantum Future

The imminent advent of quantum computing heralds a potential crisis for traditional encryption methodologies. Lattice-based FHE is inherently resistant to quantum attacks, offering a robust defence against the threat quantum computing poses to data security.

Quantum-Resistant Encryption

FHE provides a formidable layer of protection against quantum computing threats. By employing lattice-based cryptographic techniques, FHE ensures that financial data and assets remain secure even in the face of quantum adversaries.

FHE's quantum resistance is due to complex underlying math problems like the Shortest Vector Problem (SVP) and the Closest Vector Problem (CVP).These problems are believed to be intractable even for quantum computers, making lattice-based FHE an ideal candidate for post-quantum cryptography.

Using quantum-resistant encryption, like FHE, is crucial not only for protecting financial assets but also for maintaining customer trust in the digital era. As quantum computing progresses, financial institutions that prioritise robust encryption will be better positioned to navigate future challenges and opportunities.

The Future of FHE in Banking and Finance

The trajectory of FHE within the financial sector is promising, but it still faces challenges. The banking industry can tap into FHE's full potential by enhancing technology, incorporating it into daily financial operations, and cooperating with regulators.

FHE can be used in various banking and finance applications, such as:

• Secure Financial Data Analysis: FHE enables banks to analyse encrypted financial data, such as transactions, credit scores, and investment portfolios, without compromising customer privacy, ensuring secure processing of sensitive information.

• Privacy-Preserving Machine Learning: FHE allows banks to train and deploy machine learning models on encrypted data, enabling them to leverage AI for fraud detection, risk assessment, and customer segmentation while maintaining data confidentiality.

• Secure Multi-Party Computation: FHE enables secure collaboration between multiple financial institutions, allowing them to perform joint computations on encrypted data without sharing sensitive information, facilitating secure interbank transactions and compliance.

• API Security: FHE can secure APIs by encrypting sensitive data before transmission, ensuring that customer information remains confidential during data exchange between banks and third-party services.

• Secure Cloud Computing: FHE enables banks to securely outsource computations and data storage to cloud platforms without compromising data privacy, as the data remains encrypted throughout the process, expanding the use of cost-effective and scalable cloud services.

• Privacy-Preserving Regulatory Compliance: FHE allows banks to securely share encrypted data with regulatory authorities, enabling compliance with reporting requirements without exposing sensitive customer information, streamlining the compliance process while maintaining privacy.

These applications reveal the transformative power of FHE in the Banking and Financial industry and underscore its potential to revolutionise data security and privacy standards.

Overcoming Challenges in FHE Adoption

Performance Challenges and Optimisation

Addressing the computational overhead intrinsic to FHE remains a pivotal challenge. Recent progress in optimising algorithms and developing specialised hardware accelerators is narrowing the performance gap between traditional computing and fully homomorphic encryption (FHE).

Standardisation and Collaboration

The path to widespread adoption of FHE hinges on the standardisation of protocols and enhanced collaboration among stakeholders in the financial ecosystem. A unified approach towards embracing FHE can significantly accelerate its integration into mainstream financial services.

Regulation and Compliance

Regulatory bodies play a critical role in the adoption of FHE, with evolving data privacy laws mandating its use. A regulatory push could serve as a catalyst for the comprehensive adoption of FHE across the Banking and the Financial Industry industry while ensuring compliance with data protection regulations.

The regulatory landscape surrounding data privacy and security plays a significant role in the adoption of FHE within the banking industry. Strict regulations such as the General Data Protection Regulation (GDPR) and the California Consumer Privacy Act (CCPA) mandate robust data protection measures and emphasize the individual's right to privacy. FHE, with its ability to process encrypted data without decryption, aligns well with the privacy-centric focus of these regulations. As data privacy laws become increasingly stringent, FHE offers a compelling solution that enables banks to perform necessary computations and analytics while adhering to compliance requirements.

Securing Large Language Models with Fully Homomorphic Encryption (FHE)

Large Language Models (LLMs) are powerful AI tools. But their use brings up privacy concerns, especially when dealing with sensitive user data. Fully Homomorphic Encryption (FHE) provides a solution that protects user privacy and preserves model owners' intellectual property by enabling computations on encrypted data.

Privacy Challenges with LLMs

Deploying an on-premise LLM to maintain data privacy poses challenges such as high costs and potential exposure of valuable intellectual property. FHE addresses these challenges by allowing LLMs to operate on encrypted user data, ensuring privacy and model security simultaneously.

Zama's Encrypted LLM Approach

Zama ⧉, a privacy tech company, has demonstrated the feasibility of building an encrypted LLM using FHE. Their approach, which combines FHE with other privacy-enhancing technologies, achieves comparable performance to unencrypted models with only a modest increase in computational overhead.

Improving User Privacy with Encrypted LLMs

The integration of FHE into LLMs has the potential to transform user privacy, especially in applications dealing with sensitive personal or business information. As AI becomes more focused on privacy, it's important for developers, users, and regulators to work together. This collaboration is key to building an AI ecosystem that puts security and privacy first.

Conclusion

Fully Homomorphic Encryption (FHE) is a revolutionary data security technology that offers exceptional privacy and security for Banking and the Financial Industry.

As quantum computing advances, FHE becomes even more crucial. Its adoption will reshape cybersecurity in financial services, making digital banking more trustworthy and secure in our increasingly connected world.

The advent of FHE has also opened up new possibilities for secure and private use of Large Language Models. By enabling encrypted LLMs, FHE ensures that user data remains confidential while benefiting from the advanced capabilities of these models.

The Quantum Computing era is approaching. Banks must proactively assess their encryption infrastructure, identify potential vulnerabilities, and develop a clear roadmap for adopting FHE to safeguard data and maintain customer trust.